
問1 ( )個のみかんを児童に分けるのに、1人3個ずつ分けようとすると13個余り、1人5個ずつ分けようとすると9個足りません。
問2 ( )個のみかんを児童に分けるのに、男の子には1人3個ずつ、女の子には1人2個ずつ分けようとすると19個余り、男の子には1人4個ずつ、女の子には1人3個ずつ分けようとすると21個足りません。ただし男の子の人数は女の子の人数よりも4人少ないです。
解答・解説
★ ここでは「和と差に関する特殊算」とよばれる問題をご紹介します。
これらの問題文のほとんどは「定型文」といってもよいフレーズで始まり、「〇〇算」と判断して解いていく場合が多いですが、高度な中学入試算数では、あえてそこを逆手に取り、意外な展開をみせるものも多くなりますので、「実戦編」の問2ではその例をご覧いただきます。
問1
「~個のものを~人に分けるのに、1人〇個ずつ配ると☆個余り(不足し)・・・」というフレーズではじまるのは「過不足算」とよばれています。
この問題は、「過不足算」の処理で進めていきますが、ここでは様々な解き方がある中、最もポピュラーな処理法である「線分図」を使って。

上の線分図の★の部分(分ける個数の差)より、児童の数△は、
△=(13+9)÷(5-3)=11より11人とわかりますから、求めるみかんの個数は、
□=3×11+13(=5×11-9)=46より46個です。
問2
こちらも問1と同じフレーズではじまるので「過不足算」で処理しよう!となるところですが、
この問題を解くには、もう一歩工夫が必要になります。
男の子の人数をx人、女の子の人数をy人、として問1と同様に線分図に表してみます。

上の図1のような線分図で表せますが、問1とは異なり、そのあとの解き方がスムーズにいかないため、上の線分図の一部を移動させて再び線分図に表してみます。
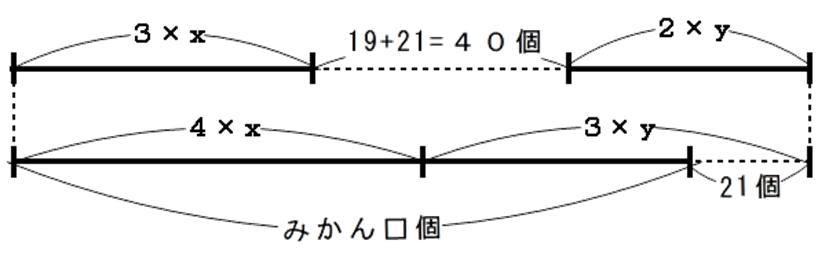
図2のような線分図で表せますが、中央の部分に着目すれば、
(4-3より)xと、(3-2より)yの和が、19+21=40となることがわかり、
x + y = 40
さらに、男の子の人数(x)は女の子の人数(y)より4人少ないことから、下の図3のようになります。

上の図3の線分図は、「和が〇、差が△」というフレーズの「和差算」となります(普通このケースは「消去算」となることが多いです)。よって、人数を求めると、
x(男の子)=(40-4)÷2=18より18人、
y(女の子)=(40+4)÷2=22より22人、
となりますので、求めるみかんの数は、
□=3×18+2×22+19(=4×18+3×22-21)
=117より117個
となります。
円周率を3.14として、以下の問いに答えなさい。
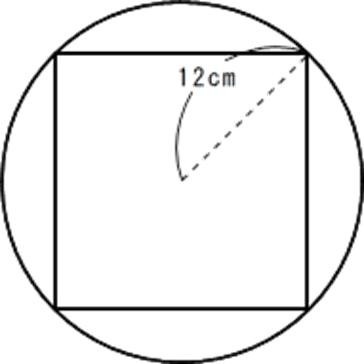
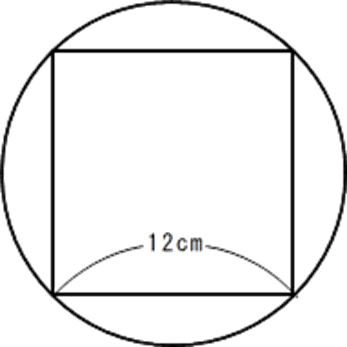
問1 下のように、半径12cmの円の周上に4つの頂点がある正方形の面積は( )cm2
です。
問2 下のように、1辺の長さが12cm
の正方形の4つの頂点が周上にある、円の面積は( )cm2
です。
★解答・解説
中学受験の算数で、すべての問題を「やり方を覚えて解く」という考えで取り組んでいると、この「図形分野」がとても難しくなり、実際この手の問題には歯が立たなくなることが多いようです。
他の分野もそうですが、「個々の問題の特徴を見抜く」姿勢を身につけて、受験を目指していただきたいところです。
問1
下のように、正方形を45度回転させた図を見てみます。
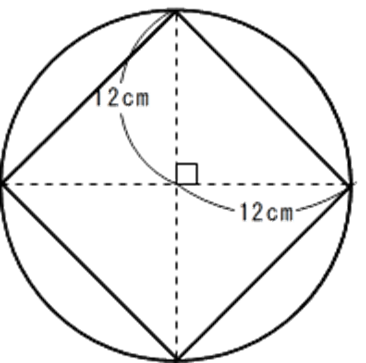
円の半径が12cmですから、円の直径は12×2=24より
24cmとなり、これが正方形の対角線となっていますので、正方形の面積は、ひし形の面積の公式を利用し、
24×24÷2=288より 288cm2
となります。
問2
問1とは逆に、正方形の1辺がわかっているときに、正方形の4つの頂点が周上にある 円の面積を求めますが、ここで受験生が間違いやすいポイントがあります。
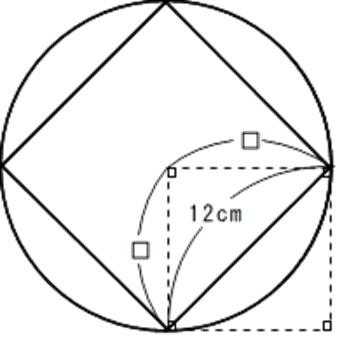
問1と同様に、正方形を45度回転させた図を見ると明らかですが、半径「□」が何cmになるのかわからないということです。
しかしこの手の問題が苦手な受験生の一部は、無理に半径を6cmにして、
6×6×3.14=113.04より113.04cm2
としてしまいますが、当然これは間違いです
※上の図でも明らかなように、□×2>12となるため、□=6cmとはなりません。
確かに半径「□」は求まりません(中学の数学では求まります)が、
半径×半径(□×□)は、問1で用いた「ひし形の面積の公式」により、
12×12÷2=72より72cm2と求まりますので、
求める円の面積は、
□×□×3.14=3.14×72
=226.08より 226.08cm2となります。
住所: 東京都中野区中野1-30-23-1F
電話: 0120-02-5335 03-5389-3995
E-mail: info@alpha-nexus.jp
受付時間: 9:00-24:00